У цій статті автор намагається відповісти на запитання: чи існує взаємозв'язок між ставленням запасів доприросту (Stock-to-Flow, або S2F) і вартістюбіткойнов. Він перевіряє запропоновану PlanB подвійну логарифмічну модель на статистичну достовірність, грунтуючись на методі найменших квадратів, на незмінність у часі кожної її змінної і на можливі хибні залежності. Векторна модель корекції помилок (VECM) створена і протестована на основі вихідної моделі відносини запасів до приросту. Хоча деякі з цих моделей з точки зору інформаційного критерію Акаіке перевершують оригінальну, всі вони не можуть спростувати гіпотезу про те, що ставлення запасів до приросту є важливим і нехибне предиктором ціни біткойнов.
Вступ
Науковий метод складний більшість людей.Він контрінтуїтивний, і тому може призвести до висновків, що не відображають думки авторів. Для того щоб зрозуміти цей метод, необхідно зрозуміти та прийняти його фундаментальну ідею:помилятися нормально. Цьому потрібно б вчити ще в школі. Якщо ми будемо боятися зробити помилку, то ніколи не зможемо запропонувати нічого нового. Історія наукових відкриттів сповнена щасливих випадковостей. Випадкові знахідки і відкриття можуть бути настільки ж (або навіть більше) важливими, ніж те, над чим вони в той момент працювали. Ідеї можуть бути помилковими або непереконливими, але те, що виявляється в процесі їх перевірки, створює фундамент для послідовників.
На переконання великого філософа науки КарлаПоппера, перевірка гіпотези її помилковість – це єдиний надійний спосіб додати ваги аргументу у тому, що вона правильна [1]. Якщо строгі багаторазові тести що неспроможні довести, що гіпотеза хибна, то з кожним таким тестом ймовірність того, що вона вірна, зростає. Ця концепція називається фальсифікованістю (або потенційною спростовністю) теорії. У цій статті я спробую сфальсифікувати модель визначення ціни біткойна на основі коефіцієнта Stock-to-Flow, описану в статті PlanB «Моделювання ціни біткойна виходячи з його дефіцитності» [2].
визначення проблеми
Щоб сфальсифікувати гіпотезу, потрібно спочатку встановити, в чому вона полягає:
Нульова гіпотеза (H0): вартість біткойнов є функцією від його коефіцієнта Stock-to-Flow
Альтернативна гіпотеза (H1): вартість біткойнов не є функцією від його коефіцієнта Stock-to-Flow
PlanB в своїй статті [2] вирішив перевірити H0,віднісши регресію звичайних найменших квадратів (OLS) на натуральний логарифм ринкової капіталізації біткойнов і натуральний логарифм коефіцієнта Stock-to-Flow. Автор не представив ні супутньої діагностики, ні будь-якої певної причини для логарифмічного перетворення обох змінних, крім ідеї про те, що подвійну логарифмічну модель можна виразити у вигляді статечної залежності. Будучи нестаціонарної, ця модель не враховує можливість встановлення помилкових залежностей.
метод
У сьогоднішній статті ми розглянемо цю модель,проведемо діагностику нормальної регресії і визначимо, чи було перетворення логарифма необхідно або доцільно (або і те, і інше), а також досліджуємо можливі втручаються фактори (конфаундери), взаємодії і чутливість.
Ще одна проблема, яку ми досліджуємо, - цепроблема нестаціонарності. Стационарность (незмінність у часі) є необхідною умовою більшості статистичних моделей. Мається на увазі ідея про те, що, якщо тренд щодо часу відсутній в середніх значеннях (або дисперсії), то він відсутній і в будь-який момент часу.
Крім аналізу стаціонарності, ми досліджуємо також можливість коінтеграції.
Умовні позначення
Традиційно розрахункове значення статистичного параметра позначається «шапкою» над символом. Тут замість нього ми використовуватимемо [ ], тобто. розрахункове значенняβ= [β].Матрицю 4×4 ми представлятимемо як [r1c1, r1c2 r2c1, r2c2] і т.д. Для позначення індексованих елементів будемо використовувати символ @ – наприклад, для 10-ї позиції у векторі X зазвичай використовується X з підрядковим індексом 10. Натомість ми будемо писати X@10.
Звичайні найменші квадрати (OLS)
Регресія звичайних найменших квадратів - це метод знаходження лінійної залежності між двома і більше змінними.
Для початку давайте визначимо лінійну модель як певну функцію X, яка дорівнює Y з деякою погрішністю.
Y = βX + ε
де Y – залежна змінна, X – незалежна змінна,ε- Це величина похибки, аβ- множникX. Завдання OLS – вивести значенняβтак, щоб мінімізуватиε.
Для того щоб вивести надійне розрахункове значення [β], Необхідно дотримати деякі основні умови:
- Наявність лінійного зв'язку між залежною і незалежною змінними
- Гомоскедастичність (тобто постійна дисперсія) помилок
- Середнє значення розподілу помилок зазвичай дорівнює нулю
- Відсутність автокореляції помилок (тобто вони не корелюють з послідовністю помилок, взятих із зсувом за часом)
лінійність
Почнемо з розгляду не перетвореного на діаграму розсіювання відносини ринкової капіталізації та коефіцієнта S2F (дані з джерела [4]).
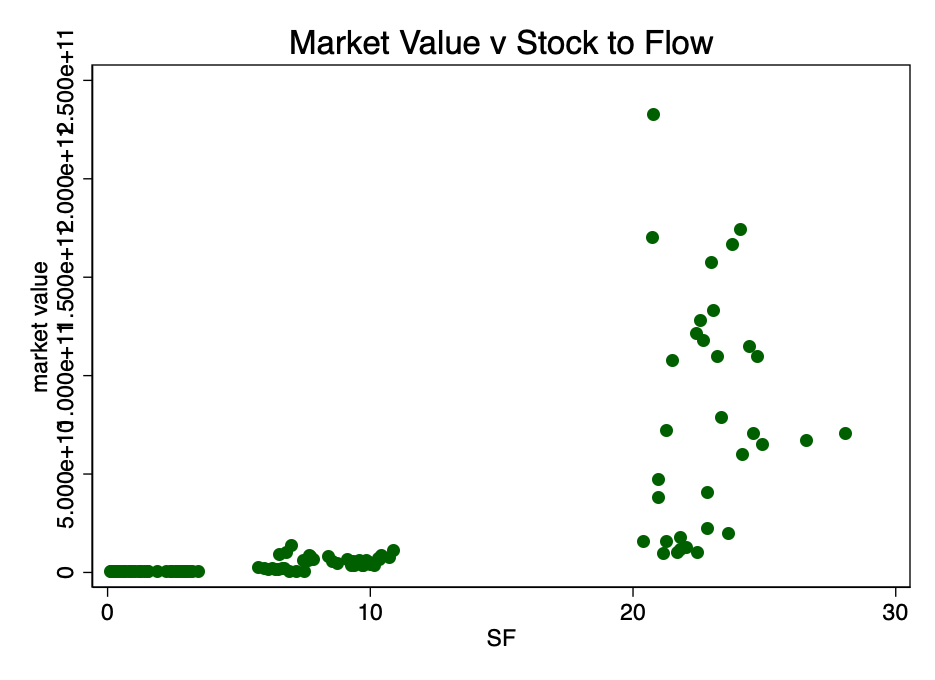
Мал. 1 - Відношення ринкової капіталізації до коефіцієнта Stock-to-Flow. Дані занадто мізерні, щоб можна було встановити взаємозв'язок.
На малюнку 1 ясно видно достатня причина длявзяття логарифма ринкової вартості: розкид значень занадто великий. При взятті логарифма від ринкової вартості (але не S2F) і повторному побудові діаграми ми отримуємо знайомий патерн (малюнок 2).
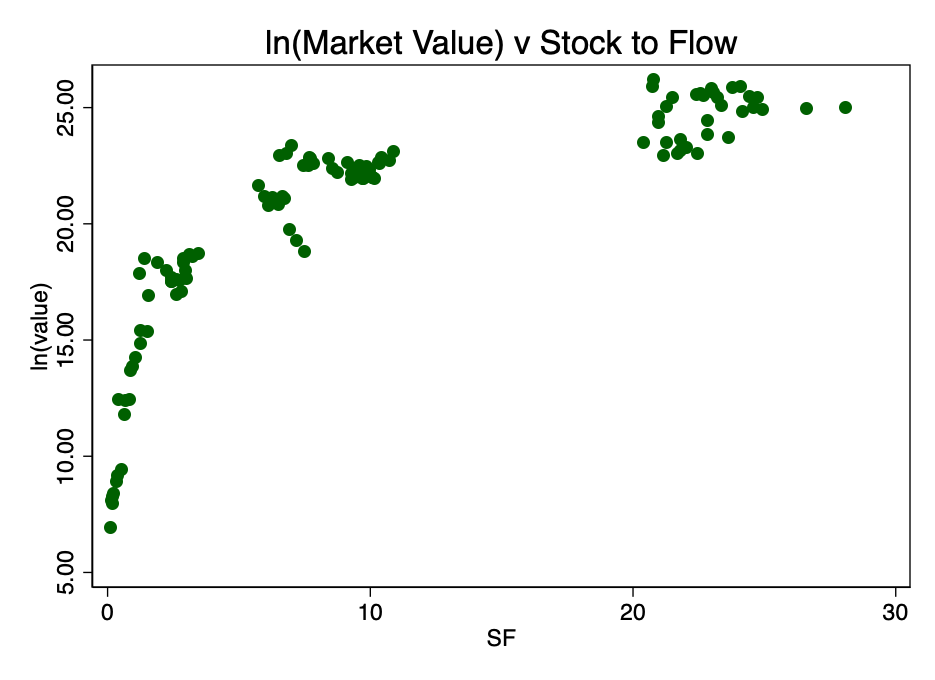
Мал. 2 - відношення логарифма ринкової капіталізації і коефіцієнта S2F. Виникає виразний логарифмический патерн.
Взявши логарифм від коефіцієнта S2F і побудувавши діаграму вже з ним, ми отримуємо очевидний лінійний патерн, ідентифікований автором джерела [2] (PlanB) на малюнку 3.
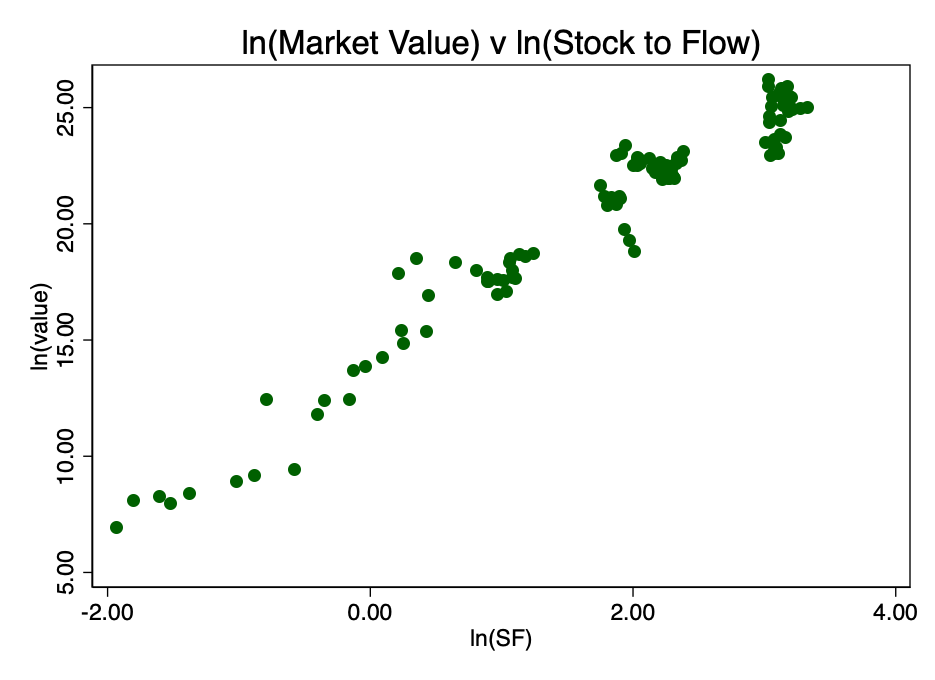
Мал. 3 - відношення логарифмів ринкової капіталізації і коефіцієнта S2F. Виникає очевидна лінійна залежність.
Це підтверджує правильність вибору подвійного логарифма як єдиного варіанта, що дає в результаті добре переглядається лінійну залежність.
Альтернативним варіантом перетворення було знаходження квадратного кореня з обох параметрів. Одержуваний при цьому патерн показаний на малюнку 4.
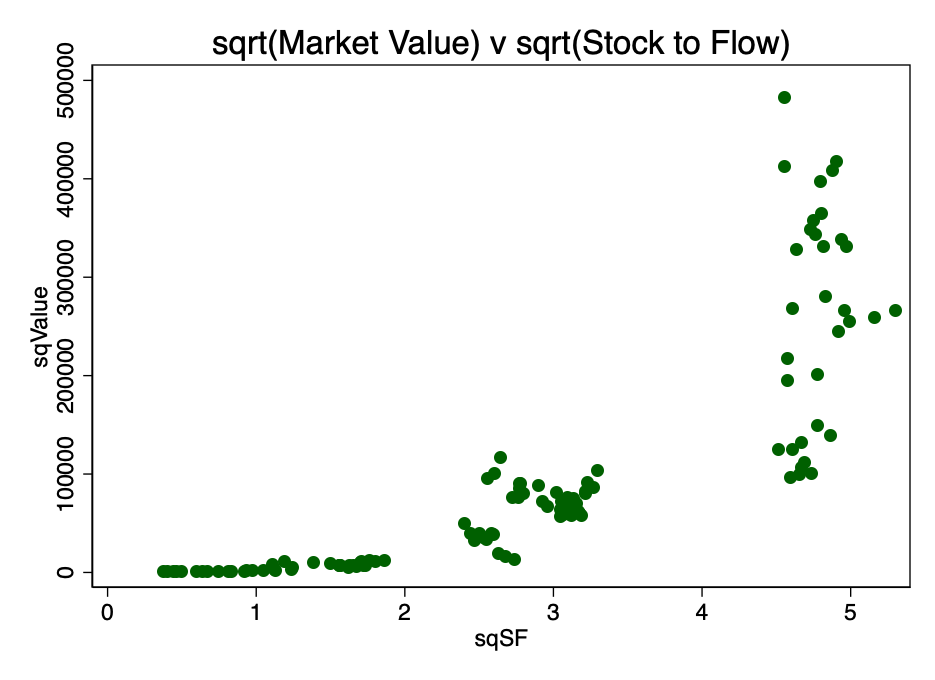
Мал. 4 - результат перетворення шляхом обчислення квадратного кореня з ринковою капіталізацією і коефіцієнта S2F.
Очевидно, що подвійне логарифмирование є найбільш підходящим перетворенням для задоволення першої умови, лінійності.
Таким чином, попередній аналіз не спростовує H0.
Результати подвійний логарифмічною регресії наведені на малюнку 5 нижче, де [β] =[3,4, 3,7](Довірчий інтервал 95%).
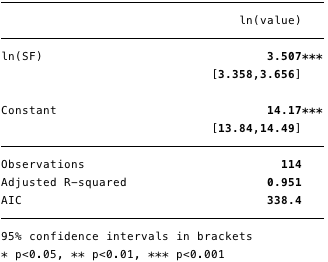
Мал. 5 - результати для подвійний логарифмічною регресії.
Використовуючи цю модель, ми тепер можемо визначити залишки [ε] І розрахункові значення [Y], А також перевірити відповідність іншим умовам.
гомоскедастичність
За дотримання умови про сталість дисперсії ввеличині похибки (тобто про гомоскедастичність), похибка для кожного значення прогнозованої вартості коливається довільним чином близько нуля. Отже, графік відношення залишкової вартості до розрахункової (рис. 6) являє собою простий, але ефективний спосіб графічно перевірити виконання цієї умови. На малюнку 6 присутній деякий патерн, а не випадкове розсіювання, що вказує на непостійність дисперсії у величині похибки (тобто на гетероскедастичність).
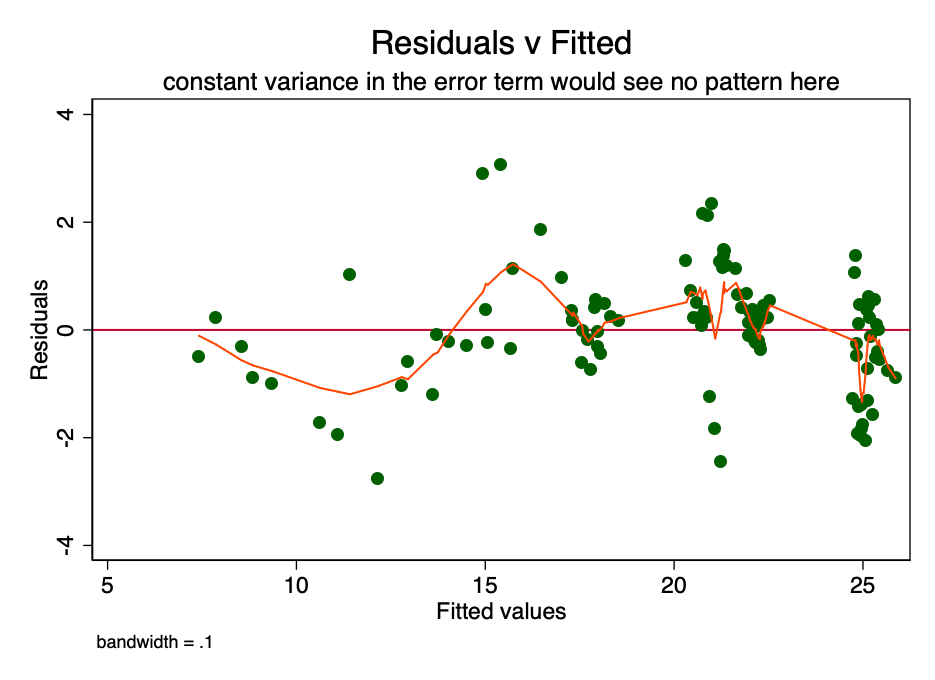
Мал. 6 - графік відносини залишкової вартості до розрахункової. При постійній дисперсії похибки, патерну не спостерігалося б. Наявність паттерна вказує на можливу проблему.
Наслідком подібної гетероскедастичності є більша дисперсія і, відповідно, менша точність розрахункових значень коефіцієнтів [β]. Крім того, вона призводить до більшої, ніж слід, значущості p-значень, оскільки метод OLS не виявляється підвищену дисперсію. Тому для розрахунку t- і F-величин ми використовуємо занижене значення дисперсії, що приводить до більш високої значимості. Це впливає також на 95% довірчий інтервал для [β], Який теж є функцією дисперсії (через стандартну похибку).
На цьому етапі можна безпечно продовжуватирегресію, віддаючи собі звіт в існуванні цих проблем. Способи впоратися з ними існують - наприклад, взяття бутстреп-вибірок або робастний оцінка дисперсії.

Мал. 7 - Вплив гетероскедастичності показано в робастний оцінюванні.
Як видно на малюнку 7, незважаючи на невеликезбільшення дисперсії (див. розширений довірчий інтервал), за великим рахунком, присутня гетероскедастичності в дійсності не робить настільки згубного впливу.
На даному етапі ми не можемо спростувати H0 через гетероскедастичності.
Нормальний розподіл помилок
Задоволення умови про те, що похибка внормі розподіляється із середнім значенням, рівним нулю, не так важливо, як задоволення умов про лінійність або гомоскедастичність. При не відповідають нормальному розподілу, але не перекручених залишках, довірчі інтервали будуть надмірно оптимістичними. Якщо ж залишки спотворені, то спотворений може бути і кінцевий результат. Однак, як видно з малюнків 8 і 9, залишки знаходяться в межах норми. Середнє значення, як здається, приблизно дорівнює нулю, і хоча формальний тест, ймовірно, спростував би гіпотезу про нормальний розподіл, залишки відповідають кривої нормального розподілу в достатній мірі, щоб довірчі інтервали не були порушені.
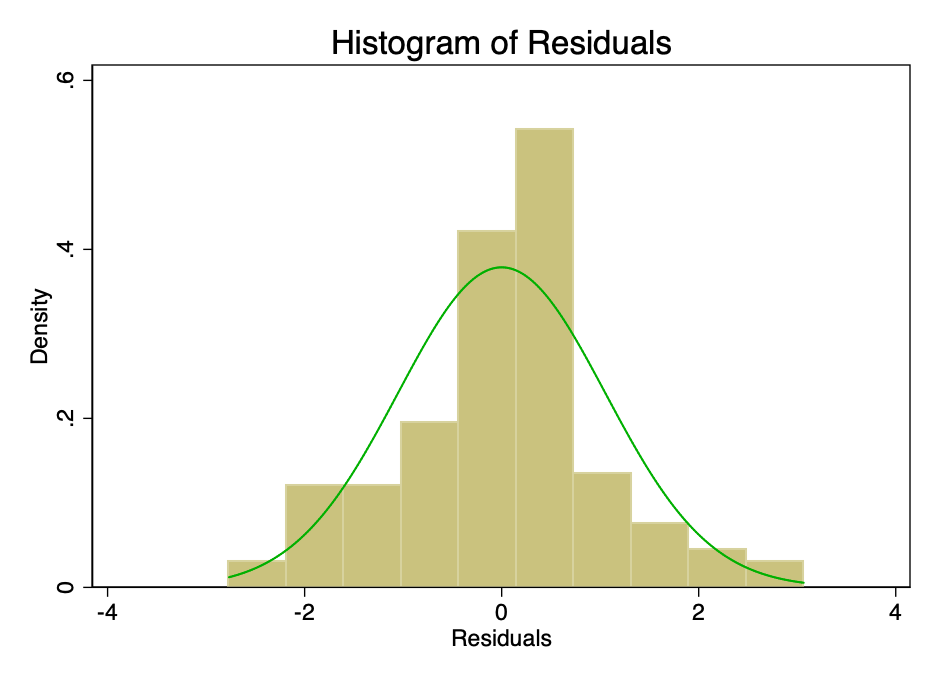
Мал. 8 - гістограма похибки з накладеною на неї (зеленої) кривої нормального розподілу.
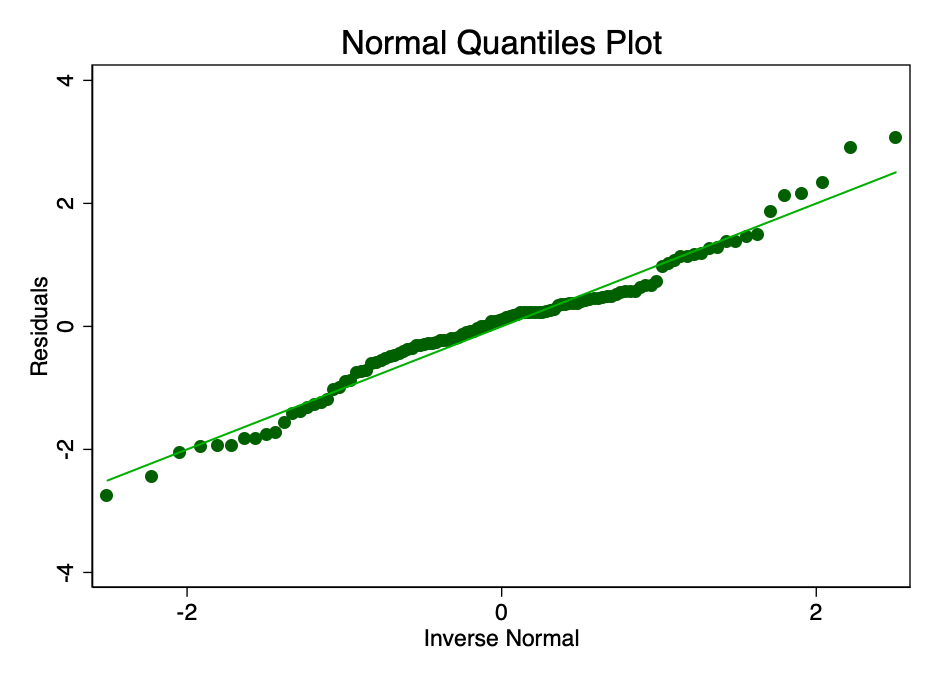
Мал. 9 - графік з нормальними Квантиль величини похибки. Чим ближче точки до лінії, тим краще нормальна підгонка.
Сила впливу (леверидж)
Леверидж тут - це концепція, згідно з якоюне всі точки даних в регресії вносять рівний внесок в оцінку коефіцієнтів. Деякі точки з високою силою впливу можуть істотно змінити коефіцієнт в залежності від того, присутні вони чи ні. На малюнку 10 ясно видно, що на ранніх етапах (березень, квітень і травень 2010 року) є кілька вселяють сумнів моментів. В цьому немає нічого дивного і PlanB в своїй статті [2] згадував про те, що збір даних за ранній період був пов'язаний з певними труднощами.
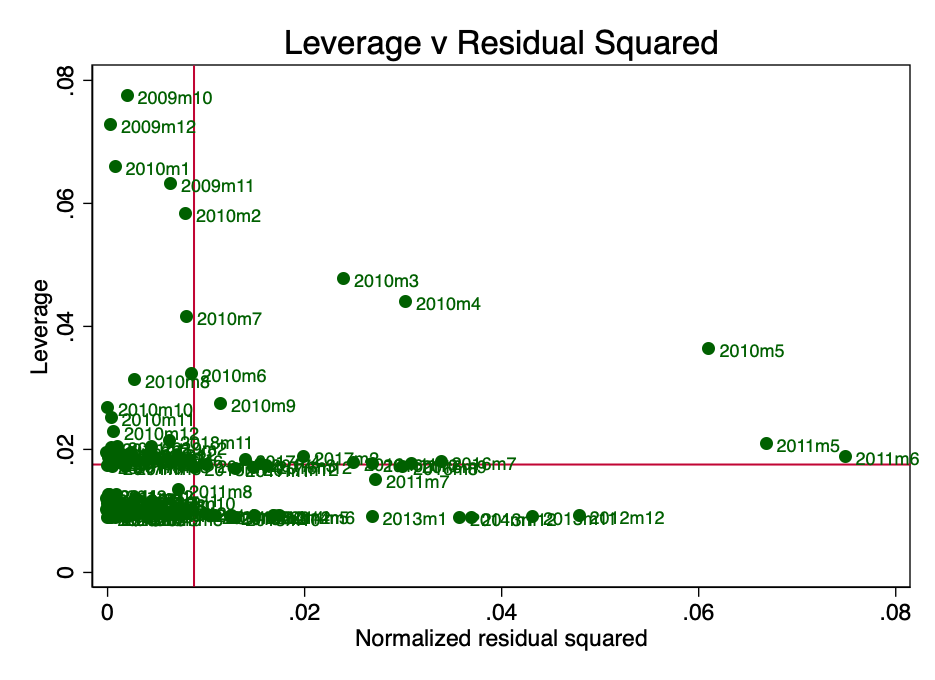
Мал. 10 - сила впливу і зведені в квадрат нормалізовані залишки.
Якщо ми повторно запускаємо регресію без цих точок (припустимо, що в них є якась помилка), то, оскільки ми знаємо про проблему гетероскедастичності, нам потрібно використовувати робастні оцінки.
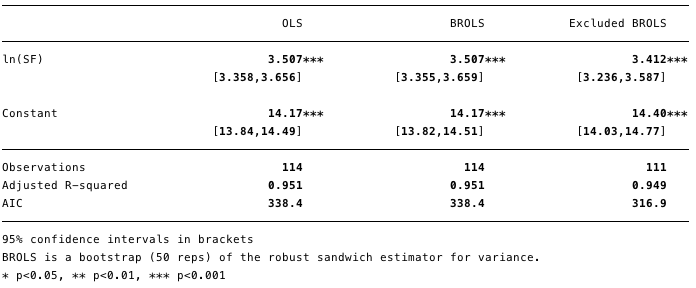
Мал. 11 - видалення точок з високою силою впливу істотно змінило розрахункове значення [β] і поліпшило значення інформаційного критерію Акаіке (AIC).
На малюнку 11 видно, що видалення цих видалення цих трьох точок значно змінює розрахункове [β] І значення інформаційного критерію Акаіке значно знижується, що говорить про те, що модель є кращою, незважаючи на більш низький R².
Резюме по OLS
Базова діагностика вказує на кілька невеликих і усунених проблем з вихідними найменшими квадратами. На цьому етапі ми не можемо спростувати H0.
стационарность
Стаціонарним називають процес із загальним порядком 0(Напр., I (0)). Нестаціонарний процес – це I(1) і більше. Обчислення інтеграла в цьому контексті – це скоріше "для бідних", сума різниць зі зсувом за часом. I(1) означає, що при відніманні першого лага з кожного значення серії виходить I(0) процес. Досить добре відомо, що регресія з нестаціонарних часових рядів може призвести до виявлення хибних зв'язків.
На малюнках 12 і 13 нижче видно, що ми не можемоспростувати нульову гіпотезу розширеного тесту Дікі-Фуллера (ADF). Нульова гіпотеза ADF-тесту полягає в тому, що дані є нестаціонарними, тобто не можна стверджувати, що дані стаціонарні.
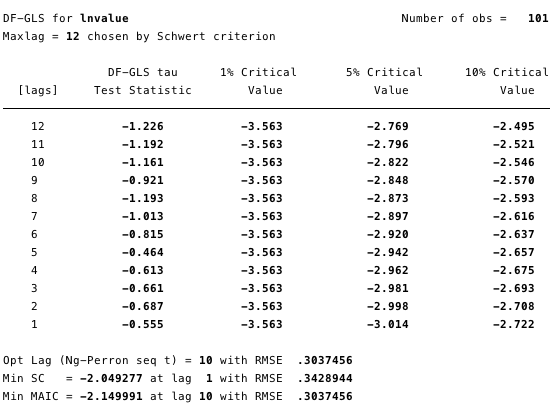
Мал. 12 - розширений тест Дікі-Фуллера для одиничного кореня на ln (вартість).
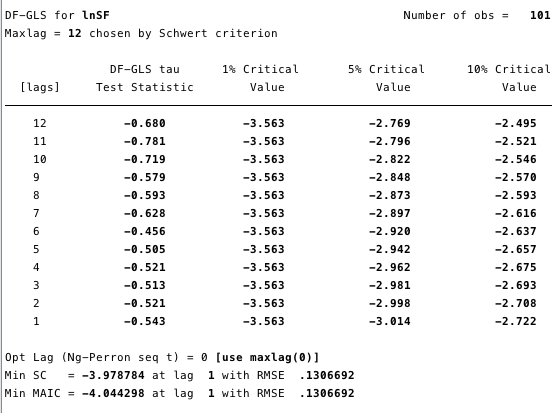
Мал. 13 - розширений тест Дікі-Фуллера для одиничного кореня на ln (S2F).
Критерій Квятковського-Філліпса-Шмідта-Шина (KPSS) – це додатковий тест на стаціонарність до тестів ADF. Нульова гіпотеза KPSS у тому, щодані є стаціонарними.Як видно на малюнках 14 і 15, ми можемо спростувати стационарность для більшості лагов в обох змінних.


Мал. 14 і 15 - KPSS-тест проти нульової гіпотези про стаціонарності.
KPSS-тести доводять, що ці дві серії, позавсяким сумнівом, є нестаціонарними. І в цьому є деяка проблема. Якщо серія не є стаціонарною щонайменше щодо тренда, то метод OLS може ідентифікувати неправдиві залежності. Єдине, що ми могли зробити - це взяти різницю між логарифмом і місячним значенням кожної змінної і перебудувати наші найменші квадрати. Однак, завдяки тому, що це питання досить широко поширений в економетричних колах, у нас є набагато більш надійний фреймворк, званий Коінтеграція.
Коінтеграція
Коінтеграція - це спосіб розібратися з парою(Або більше) процесів I (1) і визначити, чи є між ними взаємозв'язок і в чому вона полягає. В якості наочної ілюстрації коінтеграції часто наводиться спрощений приклад п'яниці і його собаки [3]. Уявіть собі п'яної людини, що прямує додому, вигулюючи на повідку собаку. П'яницю абсолютно непередбачуваним чином хитає по всій ширині дороги. Собака рухається теж досить сумбурно: обнюхує дерева, гавкає, щось риє лапами - така неспокійна собачка. Однак радіус руху собаки буде обмежений довжиною повідка, утримуваного п'яницею. Тобто можна стверджувати, що в будь-якій точці маршруту п'яниці собака буде перебувати в межах довжини повідця від нього. (Звичайно, ми не можемо передбачити, в якому напрямку від п'яниці вона буде перебувати в кожен момент часу, але вона буде в межах повідця.) Це дуже спрощена метафора коінтеграції - собака і її господар рухаються разом.
Порівняйте це з кореляцією: скажімо, бродячий собака слід за песиком п'яниці протягом 95% їх шляху, а потім тікає з гавкотом в іншу сторону за проїхав повз автомобілем. Кореляція між маршрутами бродячої собаки і п'яниці була б дуже сильною (буквально R²: 95%), однак, як і багато випадкові зв'язки п'яниці, це ставлення зовсім нічого б не означало - його не можна використовувати для прогнозування місцезнаходження п'яниці, оскільки для якогось фрагмента шляху прогноз на основі цих даних виявиться вірним, але для деяких частин він буде абсолютно неточним.
Для того щоб знайти місце розташування п'яниці, спочатку ми повинні зрозуміти, яку специфікацію порядку запізнювання слід використовувати в нашій моделі.
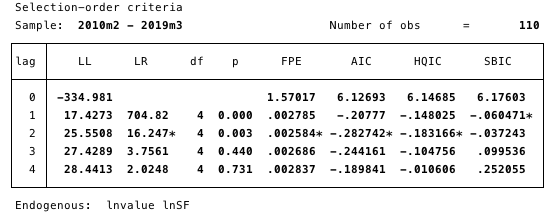
Мал. 16 - специфікація порядку запізнювання. Мінімальне значення AIC, що використовується для визначення.
Тут ми визначаємо найбільш підходящий для дослідження порядок запізнювання через вибір мінімального значення AIC близько 2.
Далі нам потрібно визначити наявність коінтегрірующего відносини. Фреймворк Йохансена [5, 6, 7] дає нам для цього чудовий інструментарій.
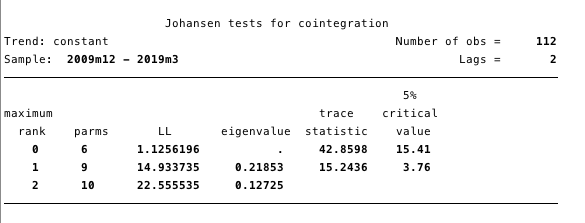
Мал. 17 - тест Йохансена на Коінтеграція.
Результати, представлені на малюнку 17, дають нам підстави стверджувати, що між ln (вартість) і ln (S2F) є принаймні одна коінтегрірующее рівняння.
Ми визначаємо нашу VECM як:
Δy@t =αβ`y@t-1+Σ(Γ@iΔy@t-1)+v+δt+ε@t
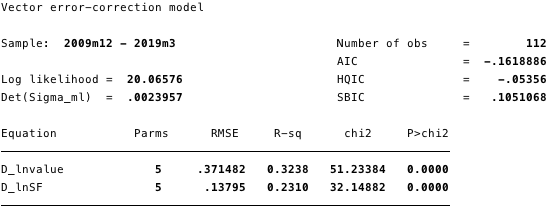
Мал. 18 - інформація про всі рівняннях моделі.
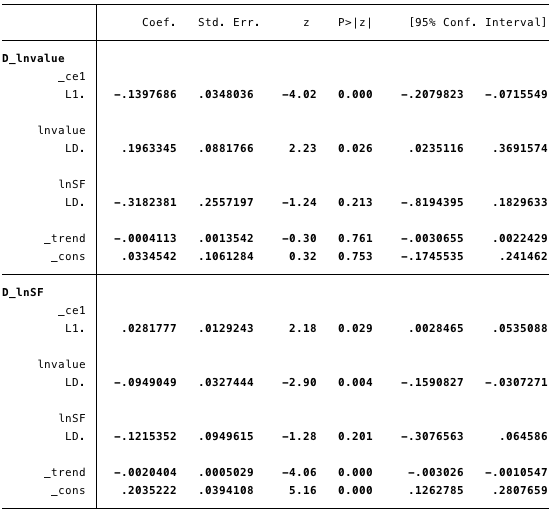
Мал. 19 - розрахункові значення короткострокових параметрів і їх статистика.

Мал. 20 - коінтегрірующее рівняння для моделі.

Мал. 21 - інформаційний критерій Акаіке для VECM.
На малюнках вище ми маємо такі розрахункові значення:
- [Α] = [-0,14, 0,03]
- [Β] = [1, -4,31],
- [V] = [0,03, 0,2] і
- [Γ] = [0,196, -0,095 -0,318, -0,122].
В цілому результат вказує на те, що модельпідходить добре. Коефіцієнт ln (S2F) в коінтеграційних рівнянні є статистично значущим, так само як і параметри коригування. Параметри коригування вказують на те, що, якщо прогнози з коінтеграційних рівняння є позитивними, то ln (вартість) знаходиться нижче свого рівноважного значення, оскільки коефіцієнт на ln (вартість) в коінтеграційних рівнянні негативний. Розрахункове значення коефіцієнта [D ln (вартість)] L. ce1 становить -0,14.
Таким чином, якщо вартість біткойнов занадтомала, вона швидко піднімається назад до рівня відповідності ln (S2F). Розрахунковий коефіцієнт [D ln (S2F)] L. ce1, рівний 0,028, має на увазі, що при дуже низькій вартості біткойнов він коригується до рівноважного рівня.
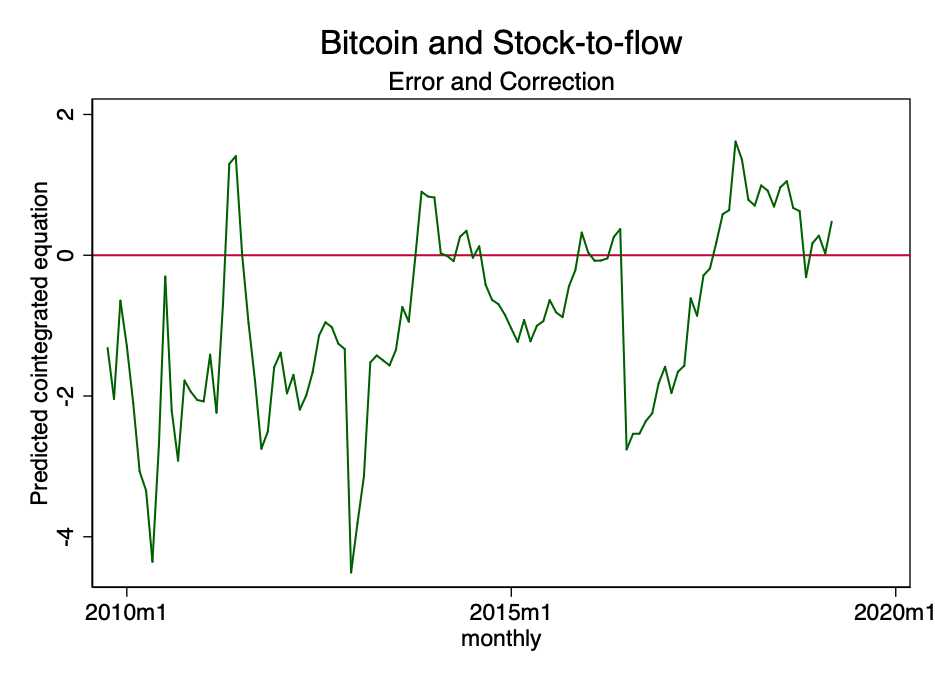
Мал. 22 - прогнозоване коінтеграційних рівняння.
На малюнку вище видно, що результат коінтеграційних рівняння має тенденцію прагнути до нуля. Хоча формально воно може бути і нестаціонарним, воно виразно прагне до стаціонарності.
З призначеного для користувача керівництва ПО Stata:
Супровідний матриця для VECM з K ендогенних(Внутрішньосистемних) змінних і r коінтеграційних рівнянь має Kr власних значень. Якщо процес стабільний, то модулі інших власних значень r складають строго менше одного. Оскільки загального розподілу для модулів власних значень немає, визначити, чи є вони занадто близькими до одиниці, може бути важко.
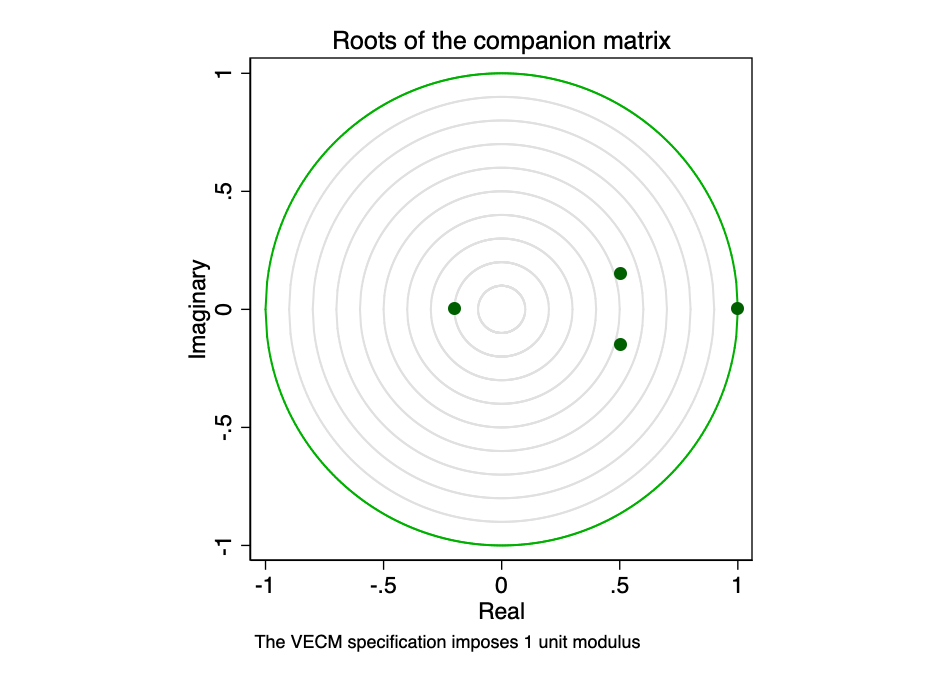
Мал. 23 - коріння супроводжує матриці.
Графічне зображення власних значеньпоказує, що жоден з решти власних значень чи не знаходиться близько до краю одиничному колі. Перевірка стійкості нашої моделі не вказує на її помилковість.
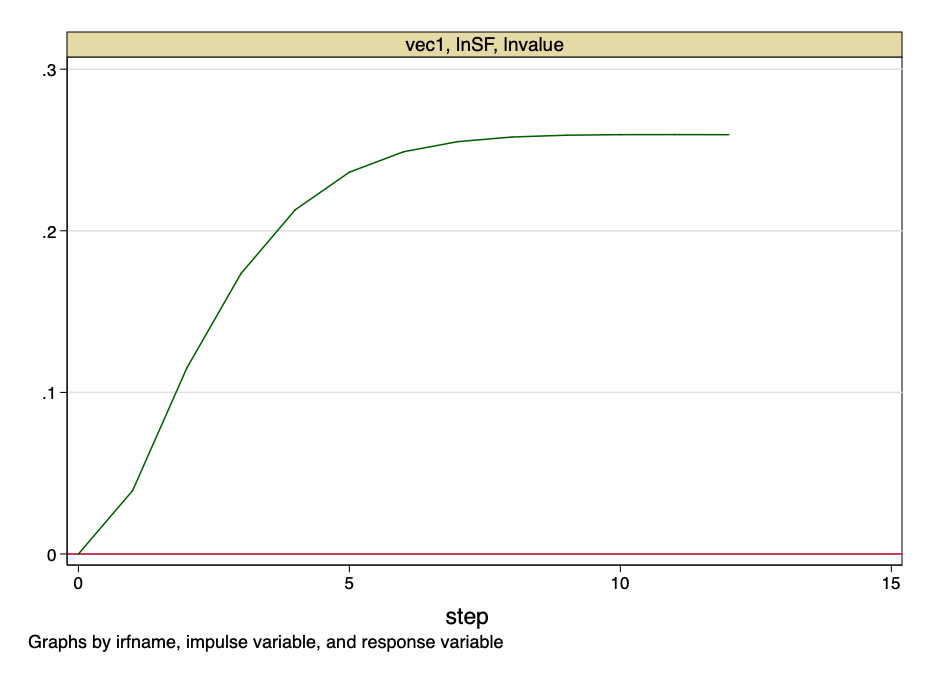
Мал. 24 - функція імпульсного відгуку.
Наведений вище малюнок вказує на те, що ортогоналізованний стрибок до значення коефіцієнта S2F чинить постійний вплив на вартість біткойнов.
І тут ми підведемо межу.Ставлення запасів до приросту не є випадковою величиною. Це функція з відомим значенням в часі. Ніяких стрибків значень S2F не буде - його вартість може бути з точністю розрахована заздалегідь. Однак ця модель дає дуже переконливі докази того, що існує фундаментальна Неложними залежність між значенням коефіцієнта S2F і вартістю біткойнов.
обмеження
У цьому дослідженні ми не враховували будь-якихфакторів, що втручаються (конфаундерів). З урахуванням наведених вище доказів, малоймовірно, щоб будь-які конфаундери могли вплинути на наш висновок – ми не можемо спростувати H0. Мине можемостверджувати, що жодної залежності між ставленням запасів до приросту та вартістю биткойна немає. Якби це було так, не було б коінтеграційного рівняння.
висновок
Хоча деякі з представлених тут моделей зточки зору інформаційного критерію Акаіке перевершують оригінальну модель PlanB, всі вони не можуть спростувати гіпотезу про те, що ставлення запасів до приросту є важливим і нехибне предиктором ціни біткойнов.
Для ілюстрації, повернемося до метафори з п'яницеюз прикладу вище: якщо порівняти вартість біткойнов з п'яницею, то коефіцієнт Stock-to-Flow - це не собака, яку він веде на повідку, але швидше за дорога, по якій він йде. П'яницю буде хитати по всій ширині дороги, іноді він буде ковзалися, пропускати повороти або навіть зрізати якісь кути, але в цілому він буде дотримуватися дороги додому.
Тобто, коротко, біткойн - це п'яниця, а відношення запасів до приросту - це дорога, по якій він йде.
цитовані матеріали
- Карл Поппер, «Логіка наукового дослідження» (1959)
- https://bitnovosti.com/2019/04/03/modelirovanie-tseny-bitkojna-ishodya-iz-ego-defitsitnosti/
- Murray, M. (1994). A Drunk and Her Dog: Ilustration of Cointegration and Error Correction.The American Statistician, 48(1), 37-39. doi: 10.2307 / 2685084
- https://github.com/100trillionUSD/bitcoin
- Johansen, S. 1988. Statistical analysis of cointegration vectors. Journal of Economic Dynamics and Control 12: 231-254.
- Johansen, S. 1991. Estimation and hypothesis testing of cointegration vectors in Gaussian vector autoregressive models. Econometrica 59: 1551-1580.
- Johansen, S. 1995. Likelihood-Based Inference in Cointegrated Vector Autoregressive Models. Oxford: Oxford University Press.
- Becketti, S. 2013. Introduction to Time Series Using Stata. College Station, TX: Stata Press.
Примітки:
- Для всіх аналізів використовувалося ПО Stata 14.
- Стаття не містить фінансових рекомендацій.
</ P>